Fem Pos Deviation Smoother

Posted on Edited on

代码来源：Apollo 6.0分支 github

配置文件

先看下平滑器的配置文件，

位置：/apollo/modules/planning/conf/discrete_points_smoother_config.txt

内容： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
max_constraint_interval : 0.25
longitudinal_boundary_bound : 2.0
max_lateral_boundary_bound : 0.5
min_lateral_boundary_bound : 0.1
curb_shift : 0.2
lateral_buffer : 0.2

discrete_points {
  smoothing_method: FEM_POS_DEVIATION_SMOOTHING
  fem_pos_deviation_smoothing {
    weight_fem_pos_deviation: 1e10
    weight_ref_deviation: 1.0
    weight_path_length: 1.0
    apply_curvature_constraint: false
    max_iter: 500
    time_limit: 0.0
    verbose: false
    scaled_termination: true
    warm_start: true
  }
}


在ReferenceLineProvider的构造函数中，有选择平滑器的相关代码：

1
2
3
4
5
6
7
8
9
10
if (smoother_config_.has_qp_spline()) {
    smoother_.reset(new QpSplineReferenceLineSmoother(smoother_config_));
  } else if (smoother_config_.has_spiral()) {
    smoother_.reset(new SpiralReferenceLineSmoother(smoother_config_));
  } else if (smoother_config_.has_discrete_points()) {
    smoother_.reset(new DiscretePointsReferenceLineSmoother(smoother_config_));
  } else {
    ACHECK(false) << "unknown smoother config "
                  << smoother_config_.DebugString();
  }

问题

参考modules/planning/math/discretized_points_smoothing/fem_pos_deviation_smoother.h代码中的注释： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*
 * @brief:
 * This class solve an optimization problem:
 * Y
 * |
 * |                       P(x1, y1)  P(x2, y2)
 * |            P(x0, y0)                       ... P(x(k-1), y(k-1))
 * |P(start)
 * |
 * |________________________________________________________ X
 *
 *
 * Given an initial set of points from 0 to k-1,  The goal is to find a set of
 * points which makes the line P(start), P0, P(1) ... P(k-1) "smooth".
 */
即平滑一系列的离散点

#### 原理

原理和公式可以参考这篇讲解，非常详细：https://zhuanlan.zhihu.com/p/342740447

Three quadratic penalties are involved:

  1. Penalty x on distance between middle point and point by finite element estimate;
  2. Penalty y on path length;
  3. Penalty z on difference between points and reference points

costX : \(\sum ((p_1 + p_3) - 2*p_2)^2\)

costY : \(\sum (p_{n+1} - p_n)^2\)

costZ : \(\sum (p_n - p_{refn})^2\)

General formulation of P matrix is as below(with 6 points as an example): I is a two by two identity matrix, X, Y, Z represents x * I, y * I, z * I 0 is a two by two zero matrix

\[\begin{vmatrix} X+Y+Z&-2X-Y&X&0&0&0\\ 0&5X+2Y+Z&-4X-Y&X&0&0\\ 0&0&6X+2Y+Z&-4X-Y&X&0\\ 0&0&0&6X+2Y+4Z&-4X-Y&X\\ 0&0&0&0&5X+2Y+Z&-2X-Y\\ 0&0&0&0&0&X+Y+Z\\ \end{vmatrix}\]

Only upper triangle needs to be filled

#### 示例代码 用10个点模拟测试一下效果： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
import osqp
import numpy as np
import matplotlib.pyplot as plt
%matplotlib widget
from scipy import sparse

#add some data for test
x_array = [0.5,1.0,2.0,3.0,4.0,
           5.0,6.0,7.0,8.0,9.0,
          10.0,11.0,12.0,13.0,14.0,
          15.0,16.0,17.0,18.0,19.0]
y_array = [0.1,0.3,0.2,0.4,0.3,
           -0.2,-0.1,0,0.5,0,
          0.1,0.3,0.2,0.4,0.3,
           -0.2,-0.1,0,0.5,0]
length = len(x_array)

#weight , from config
weight_fem_pos_deviation_ = 1e10 #cost1 - x
weight_path_length = 1          #cost2 - y
weight_ref_deviation = 1        #cost3 - z


P = np.zeros((length,length))
#set P matrix,from calculateKernel
#add cost1
P[0,0] = 1 * weight_fem_pos_deviation_
P[0,1] = -2 * weight_fem_pos_deviation_
P[1,1] = 5 * weight_fem_pos_deviation_
P[length - 1 , length - 1] = 1 * weight_fem_pos_deviation_
P[length - 2 , length - 1] = -2 * weight_fem_pos_deviation_
P[length - 2 , length - 2] = 5 * weight_fem_pos_deviation_

for i in range(2 , length - 2):
    P[i , i] = 6 * weight_fem_pos_deviation_
for i in range(2 , length - 1):
    P[i - 1, i] = -4 * weight_fem_pos_deviation_
for i in range(2 , length):
    P[i - 2, i] = 1 * weight_fem_pos_deviation_
    
with np.printoptions(precision=0):
    print(P)
    
P = P / weight_fem_pos_deviation_
P = sparse.csc_matrix(P)

#set q matrix , from calculateOffset
q = np.zeros(length)

#set Bound(upper/lower bound) matrix , add constraints for x
#from CalculateAffineConstraint

#In apollo , Bound is from road boundary,
#Config limit with (0.1,0.5) , Here I set a constant 0.2 
bound = 0.2
A = np.zeros((length,length))
for i in range(length):
    A[i, i] = 1
A = sparse.csc_matrix(A)
lx = np.array(x_array) - bound
ux = np.array(x_array) + bound
ly = np.array(y_array) - bound
uy = np.array(y_array) + bound

#solve
prob = osqp.OSQP()
prob.setup(P,q,A,lx,ux)
res = prob.solve()
opt_x = res.x

prob.update(l=ly, u=uy)
res = prob.solve()
opt_y = res.x

#plot x - y , opt_x - opt_y , lb - ub

fig1 = plt.figure(dpi = 100 , figsize=(12, 8))
ax1_1 = fig1.add_subplot(2,1,1)

ax1_1.plot(x_array,y_array , ".--", color = "grey", label="orig x-y")
ax1_1.plot(opt_x, opt_y,".-",label = "opt x-y")
# ax1_1.plot(x_array,ly,".--r",label = "bound")
# ax1_1.plot(x_array,uy,".--r")
ax1_1.legend()
ax1_1.grid(axis="y",ls='--')


#计算kappa用来评价曲线
def calcKappa(x_array,y_array):
    s_array = []
    k_array = []
    if(len(x_array) != len(y_array)):
        return(s_array , k_array)
    
    length = len(x_array)
    temp_s = 0.0
    s_array.append(temp_s)
    for i in range(1 , length):
        temp_s += np.sqrt(np.square(y_array[i] - y_array[i - 1]) + np.square(x_array[i] - x_array[i - 1]))
        s_array.append(temp_s)

    xds,yds,xdds,ydds = [],[],[],[]
    for i in range(length):
        if i == 0:
            xds.append((x_array[i + 1] - x_array[i]) / (s_array[i + 1] - s_array[i]))
            yds.append((y_array[i + 1] - y_array[i]) / (s_array[i + 1] - s_array[i]))
        elif i == length - 1:
            xds.append((x_array[i] - x_array[i-1]) / (s_array[i] - s_array[i-1]))
            yds.append((y_array[i] - y_array[i-1]) / (s_array[i] - s_array[i-1]))
        else:
            xds.append((x_array[i+1] - x_array[i-1]) / (s_array[i+1] - s_array[i-1]))
            yds.append((y_array[i+1] - y_array[i-1]) / (s_array[i+1] - s_array[i-1]))
    for i in range(length):
        if i == 0:
            xdds.append((xds[i + 1] - xds[i]) / (s_array[i + 1] - s_array[i]))
            ydds.append((yds[i + 1] - yds[i]) / (s_array[i + 1] - s_array[i]))
        elif i == length - 1:
            xdds.append((xds[i] - xds[i-1]) / (s_array[i] - s_array[i-1]))
            ydds.append((yds[i] - yds[i-1]) / (s_array[i] - s_array[i-1]))
        else:
            xdds.append((xds[i+1] - xds[i-1]) / (s_array[i+1] - s_array[i-1]))
            ydds.append((yds[i+1] - yds[i-1]) / (s_array[i+1] - s_array[i-1]))
    for i in range(length):
        k_array.append((xds[i] * ydds[i] - yds[i] * xdds[i]) / (np.sqrt(xds[i] * xds[i] + yds[i] * yds[i]) * (xds[i] * xds[i] + yds[i] * yds[i]) + 1e-6));
    return(s_array,k_array)


#plot kappa
ax1_2 = fig1.add_subplot(2,1,2)
s_orig,k_orig = calcKappa(x_array,y_array)
s_opt ,k_opt = calcKappa(opt_x,opt_y)
ax1_2.plot(s_orig , k_orig , ".--", color = "grey", label="orig s-kappa")
ax1_2.plot(s_opt,k_opt,".-",label="opt s-kappa")
ax1_2.legend()
ax1_2.grid(axis="y",ls='--')
查看结果：
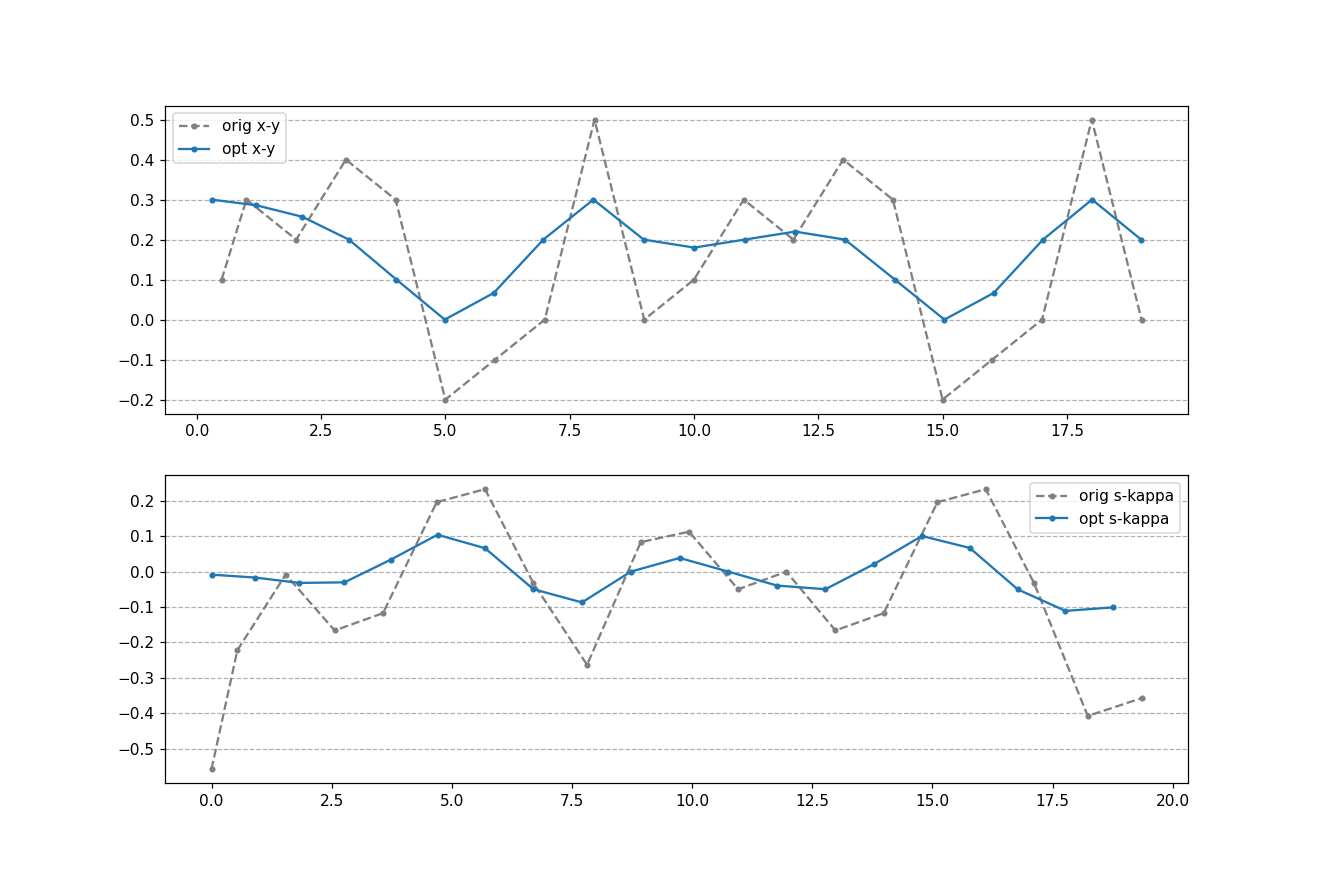
cW75ND.png
上图灰线为原曲线，蓝色为平滑后的曲线
下图灰线为原曲线kappa，蓝线为平滑后的kappa
可以看出平滑效果还不错。

使用测试数据再跑一下：

cWHR2j.png

平滑前后的kappa对比非常明显

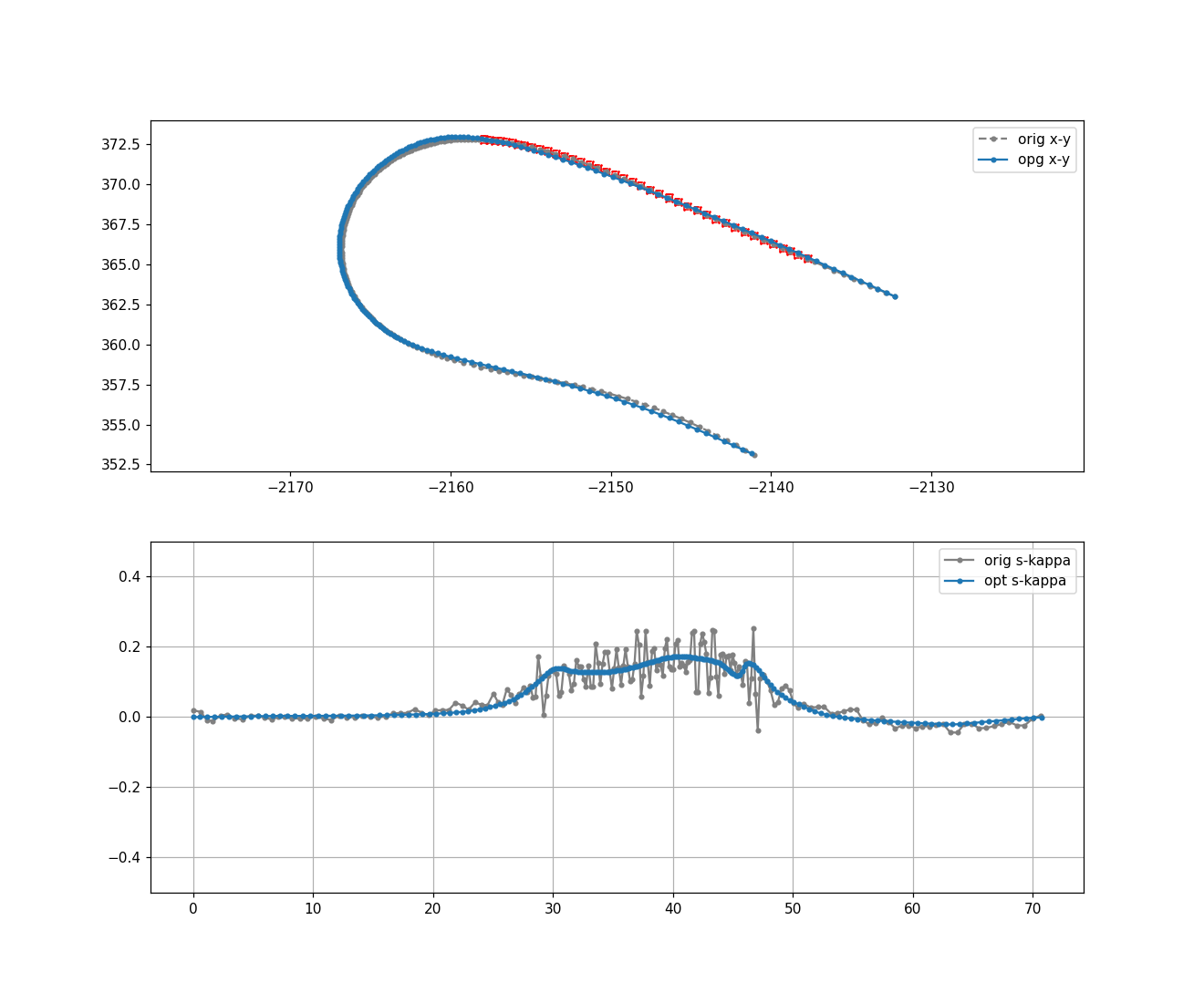
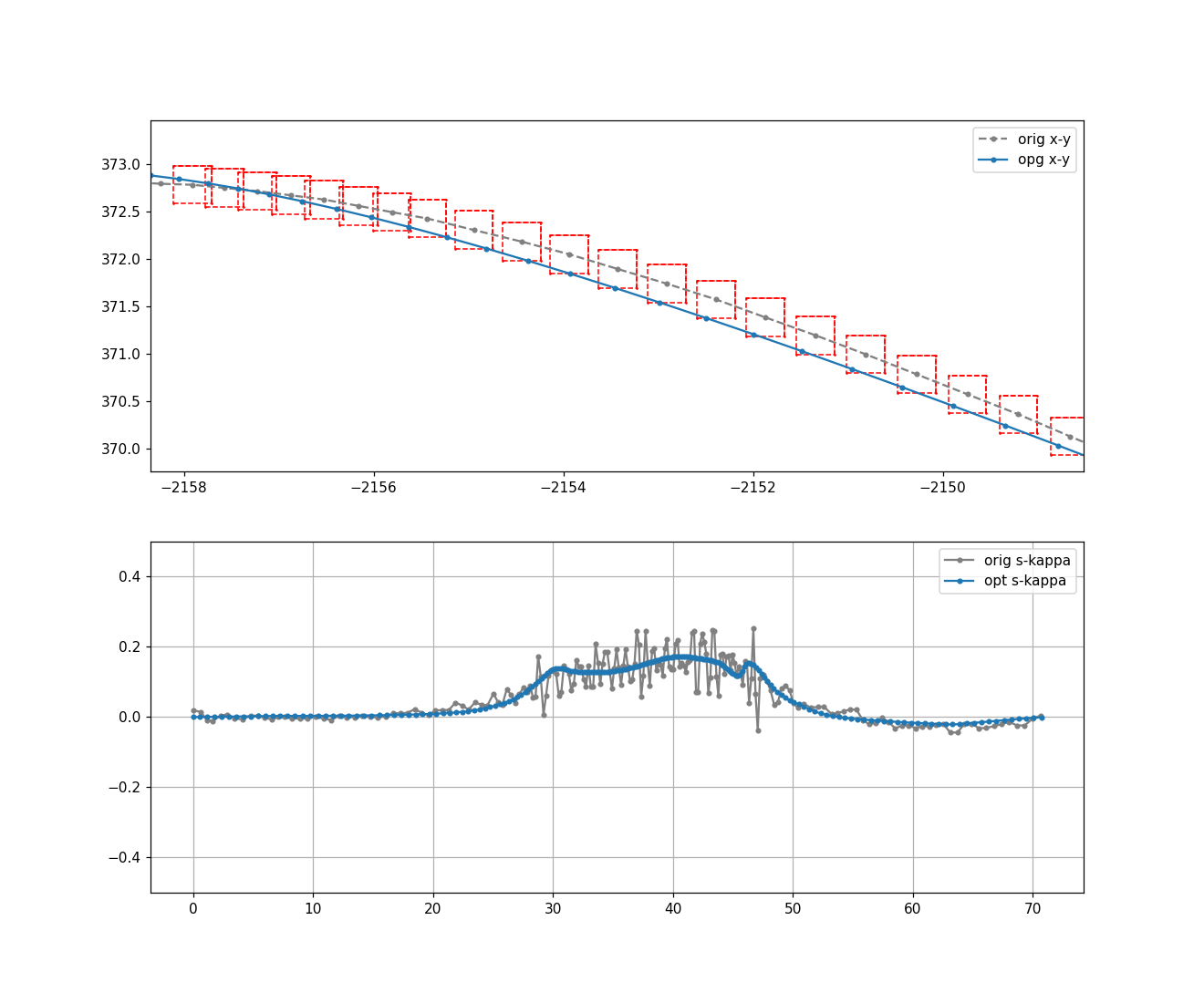
将bound也画出来：

cWbPiD.png

原曲线上的每个点，都生成一个矩形。

在该矩形中迭代求解使cost最小的点。